Author: jcblackmon

The Isotacheian Model: An Alternative Explanation of Velocity Time Dilation Measurements

In our special theory of relativity (STR), time dilates for physical systems in uniform motion relative to observers. For instance, if a physical system is moving at 0.8 the speed of light relative to us, we observe it changing state at 0.6 the rate we change state, and if the system is a starship with a clock onboard, we measure that clock ticking 36 times for our clock’s 60 ticks. In STR, this phenomenon is called time dilation, and it has been confirmed by a wealth of empirical data going back to Rossi-Hall (1940) and Frisch-Smith (1962). The standard explanation, based on Einstein’s two postulates, is regarded as non-classical.

What if there were also a simple, even classical, kinematic explanation of our time dilation measurements? What if it could be shown that decreases in the rate at which systems change intrinsically follow for purely kinematic reasons from a single postulate? Here begins a presentation of the isotacheian model in the form of videos, 3D models, and documents. This presentation and the playlist are currently under construction.

Find my recently published article on this model here.

Here is a playlist of four short videos, each under five minutes, explaining the isotacheian model.

Dynamic Models

Unfortunately, these models do not perform especially well on some smartphones.

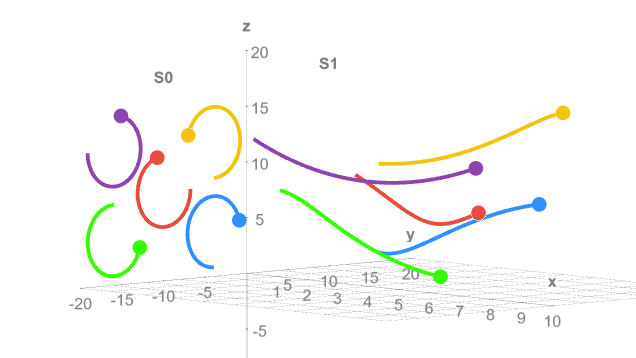
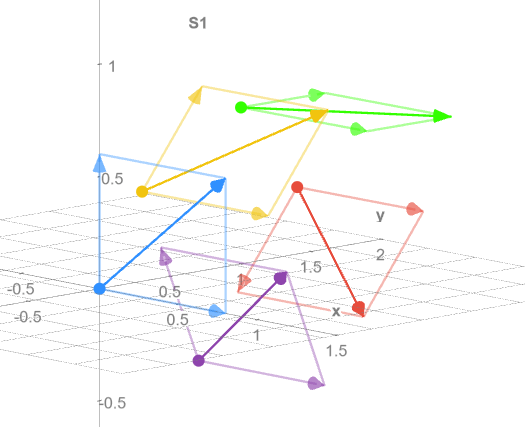
  • Five Particles Set v to any value in the range [0,1] to see the Pythagorean relation between an isotacheian system’s speed in R and the rate at which its particles can move relative to each other and thus the rate at which it can change intrinsic state.
  • Helical Paths Set v to any value in the range [0,1] to see how the rate of intrinsic change for S1 compares to that rate for S0, which is at rest in frame R. The isotacheian model does not require helical paths to work, but they can make the Pythagorean-Lorentzian relation intuitive, and they have some justification in physics.

Briefly…

A system is isotacheian if and only if there is a reference frame R in which all particles always have equal speed in R. Isotacheian systems exhibit a kinematic form of time dilation.
The relation between an isotacheian system’s speed and the maximum rate at which it can change state is Pythagorean. (The colors and assignments unfortunately do not match those in the previous image; this is a new set of particles.) The vectors parallel to the x-axis are all the same (a convenient idealization), resulting in S1 having that instantaneous velocity. It follows that the maximum rate at which S1 can change state is determined by this Pythagorean relation.
A Lorentz equivalent follows. But instead of time t dilating, the rate of change i for isotacheian systems decreases as their speed in R increases. The time dilation measurements we have made follow for straightforward, even classical, kinematic reasons.

Commentary

Here, I will elaborate on questions raised, points needing clarification, and potential problems and objections.

  • What are s-particles?
  • The isotacheian model permits but does not require an aether. (Coming soon.)
  • Vector Analysis vs. Vector Addition (Coming soon.)
  • (More planned.)

Other Sources

In recent years, I have discovered some fellow isotacheians whom I name in the introductory video. Here are some links to them and their work.

0

Experimenting with Adelson’s Checkerboard Illusion

Can you change how things seem? Phenomenological slideshow test below! Scroll past all the text (if you must).

Edward H. Adelson‘s (1995) Checkerboard Illusion, or “Checkershadow Illusion“, remains one of the best lessons on how deceptive our perceptions can be, and it affords a great opportunity for phenomenological experimentation, which I promote with a slideshow below. Above is an inspired variation on Adelson’s original by a digital artist who goes by butisit at DeviantArt. Continue reading “Experimenting with Adelson’s Checkerboard Illusion” →

The Wada Test for Philosophers: What is it like to be a proper part of your own brain losing and regaining other proper parts of your brain?

Evidently, good answers to this question are not confined to the wilds of science fiction and thought experiment. In fact, I think there are actually people with a pretty good idea: patients of the Wada test.
These are people who have had their brain hemispheres anesthetized one at a time so that the rest of the brain—the complementary other hemisphere and the subcortical regions—remains functioning in some ways, and by all accounts conscious. Some of these patients report on their conscious experiences afterward, for example, describing what it is like to have one’s language dominant hemisphere temporarily shut down, finding oneself at a complete—albeit only temporary—loss of words. Continue reading “The Wada Test for Philosophers: What is it like to be a proper part of your own brain losing and regaining other proper parts of your brain?” →

Was the Liar solved?

I vaguely recall that somewhere Karl Popper expresses his suspicion that some philosophers are unwilling to accept a solution to a challenging problem because they have become so fond of the problem. I wonder if this applies to the Liar Paradox and a “simple solution” that Eugene Mills supports. As Mills sees it (and I’m effectively convinced) the Liar is not paradoxical, but plain false, and though it appears to truthfully say it is false, it does not truthfully say so. So it’s just false. Continue reading “Was the Liar solved?” →

Thinking about Rights to Freedoms

A right is a normative rule establishing that society owes or allows something to certain parties. Some rights guarantee freedoms. Rights to freedoms are the focus here. When thinking about freedom it is useful to keep in mind that freedom is not a simple property that an individual may or may not have, nor is it a simple state of affairs that may or may not hold in a society. Freedom is instead a complex relation with variables that need specification. Continue reading “Thinking about Rights to Freedoms” →

Rosenblatt’s Perceptron

Frank Rosenblatt was pioneering neural networks and connectionist machine learning in the 1950s with the Mark I Perceptron. While the term perceptron now refers primarily to a learning algorithm, Rosenblatt’s perceptron was the physical machine that executed it.

In a 1958 New York Times article (below), Rosenblatt conveys an ambitious (prescient?) vision of the future of machine learning. The article refers to Rosenblatt’s perceptron as “the embryo of an electronic computer that [the Navy] expects will be able to walk, talk, see, write, reproduce itself and be conscious of its existence.” Continue reading “Rosenblatt’s Perceptron” →

Create a website or blog at WordPress.com

Up ↑